Appendix B to Part 434 - Baseline Determination and Compliance Monitoring for Pre-existing Discharges at Remining Operations
40:32.0.1.1.10.8.4.7.6 : Appendix B
Appendix B to Part 434 - Baseline Determination and Compliance
Monitoring for Pre-existing Discharges at Remining Operations I.
General Procedure Requirements
a. This appendix presents the procedures to be used for
establishing effluent limitations for pre-existing discharges at
coal remining operations, in accordance with the requirements set
forth in subpart G; Coal Remining. The requirements specify that
pollutant loadings of total iron, total manganese, total suspended
solids, and net acidity in pre-existing discharges shall not exceed
baseline pollutant loadings. The procedures described in this
appendix shall be used for determining site-specific, baseline
pollutant loadings, and for determining whether discharge loadings
during coal remining operations have exceeded the baseline loading.
Both a monthly (single-observation) procedure and an annual
procedure shall be applied, as described below.
b. In order to sufficiently characterize pollutant loadings
during baseline determination and during each annual monitoring
period, it is required that at least one sample result be obtained
per month for a period of 12 months.
c. Calculations described in this appendix must be applied to
pollutant loadings. Each loading value is calculated as the product
of a flow measurement and pollutant concentration taken on the same
date at the same discharge sampling point, using standard units of
flow and concentration (to be determined by the permitting
authority). For example, flow may be measured in cubic feet per
second, concentration in milligrams per liter, and the pollutant
loading could be calculated in pounds per year.
d. Accommodating Data Below the Maximum Daily Limit at subpart C
of this part. In the event that a pollutant concentration in the
data used to determine baseline is lower than the daily maximum
limitation established in subpart C of this part for active mine
wastewater, the statistical procedures should not establish a
baseline more stringent than the BPT and BAT effluent standards
established in subpart C of this part. Therefore, if the total iron
concentration in a baseline sample is below 7.0 mg/L, or the total
manganese concentration is below 4.0 mg/L, the baseline sample
concentration may be replaced with 7.0 mg/L and 4.0 mg/L,
respectively, for the purposes of some of the statistical
calculations in this appendix B. The substituted values should be
used for all methods in this appendix B with the exception of the
calculation of the interquartile range (R) in Method 1 for the
annual trigger (Step 3), and in Method 2 for the single observation
trigger (Step 3). The interquartile range (R) is the difference
between the quartiles M−1 and M1; these values should be calculated
using actual loadings (based on measured concentrations) when they
are used to calculate R. This should be done in order to account
for the full range of variability in the data.
II. Procedure for Calculating and Applying a Single-Observation
(Monthly) Trigger
Two alternative methods are provided for calculating a
single-observation trigger. One method must be selected and applied
by the permitting authority for any given remining permit.
A. Method 1 for Calculating a Single Observation Trigger (L)
(1) Count the number of baseline observations taken for the
pollutant of interest. Label this number n. In order to
sufficiently characterize pollutant loadings during baseline
determination and during each annual monitoring period, it is
required that at least one sample result be obtained per month for
a period of 12 months.
(2) Order all baseline loading observations from lowest to
highest. Let the lowest number (minimum) be x(1), the next lowest
be x(2), and so forth until the highest number (maximum) is
x(n).
(3) If fewer than 17 baseline observations were obtained, then
the single observation trigger (L) will equal the maximum of the
baseline observations (x(n)).
(4) If at least 17 baseline observations were obtained,
calculate the median (M) of all baseline observations:
Instructions for calculation of a median of n observations:
If n is odd, then M equals x(n/2 + 1/2).
For example, if there are 17 observations, then M = X(17/2 +
1/2) = x(9), the 9th highest observation.
If n is even, then M equals 0.5 * (x(n/2) + x(n/2 + 1)).
For example, if there are 18 observations, then M equals 0.5
multiplied by the sum of the 9th and 10th highest observations.
(a) Next, calculate M1 as the median of the subset of
observations that range from the calculated M to the maximum x(n);
that is, calculate the median of all x larger than or equal to
M.
(b) Next, calculate M2 as the median of the subset of
observations that range from the calculated M1 to x(n) ; that is,
calculate the median of all x larger than or equal to M1.
(c) Next, calculate M3 as the median of the subset of
observations that range from the calculated M2 to x(n) ; that is,
calculate the median of all x larger than or equal to M2.
(d) Finally, calculate the single observation trigger (L) as the
median of the subset of observations that range from the calculated
M3 to x(n).
Note:
When subsetting the data for each of steps 3a-3d, the subset
should include all observations greater than or equal to the median
calculated in the previous step. If the median calculated in the
previous step is not an actual observation, it is not included in
the new subset of observations. The new median value will then be
calculated using the median procedure, based on whether the number
of points in the subset is odd or even.
(5) Method for applying the single observation trigger (L) to
determine when the baseline level has been exceeded
If two successive monthly monitoring observations both exceed L,
immediately begin weekly monitoring for four weeks (four weekly
samples).
(a) If three or fewer of the weekly observations exceed L,
resume monthly monitoring
(b) If all four weekly observations exceed L, the baseline
pollution loading has been exceeded.
B. Method 2 for Calculating a Single Observation Trigger (L)
(1) Follow Method 1 above to obtain M1 (the third quartile, that
is, the 75th percentile).
(2) Calculate M−1 as the median of the baseline data which are
less than or equal to the sample median M.
(3) Calculate interquartile range, R = (M1 − M−1).
(4) Calculate the single observation trigger L as
L = M1 + 3 * R
(5) If two successive monthly monitoring observations both
exceed L, immediately begin weekly monitoring for four weeks (four
weekly samples).
(a) If three or fewer of the weekly observations exceed L,
resume monthly monitoring
(b) If all four weekly observations exceed L, the baseline
pollution loading has been exceeded.
III. Procedure for Calculating and Applying an Annual Trigger A.
Method 1 for Calculating and Applying an Annual Trigger (T)
(1) Calculate M and M1 of the baseline loading data as described
above under Method 1 for the single observation trigger.
(2) Calculate M−1 as the median of the baseline data which are
less than or equal to the sample median M.
(3) Calculate the interquartile range, R = (M1 − M−1).
(4) The annual trigger for baseline (Tb) is calculated as:
where n is the number of baseline loading
observations.
(5) To compare baseline loading data to observations from the
annual monitoring period, repeat steps 1-3 for the set of
monitoring observations. Label the results of the calculations M′
and R′. Let m be the number of monitoring observations.
(6) The subtle trigger (Tm) of the monitoring data is calculated
as:
(7) If Tm >Tb, the median loading of the monitoring
observations has exceeded the baseline loading.
B. Method 2 for Calculating and Applying an Annual Trigger (T)
Method 2 applies the Wilcoxon-Mann-Whitney test to determine
whether the median loading of the monitoring observations has
exceeded the baseline median. No baseline value T is
calculated.
(1) Steps for Conducting the Wilcoxon-Mann-Whitney Test
(a) Let n be the number of baseline loading observations taken,
and let m be the number of monitoring loading observations taken.
In order to sufficiently characterize pollutant loadings during
baseline determination and during each annual monitoring period, it
is required that at least one sample result be obtained per month
for a period of 12 months.
(b) Order the combined baseline and monitoring observations from
smallest to largest.
(c) Assign a rank to each observation based on the assigned
order: the smallest observation will have rank 1, the next smallest
will have rank 2, and so forth, up to the highest observation,
which will have rank n + m.
(1) If two or more observations are tied (have the same value),
then the average rank for those observations should be used. For
example, suppose the following four values are being ranked:
3, 4, 6, 4 Since 3 is the lowest of the four numbers, it would be
assigned a rank of 1. The highest of the four numbers is 6, and
would be assigned a rank of 4. The other two numbers are both 4.
Rather than assign one a rank of 2 and the other a rank of 3, the
average of 2 and 3 (
i.e., 2.5) is given to both numbers.
(d) Sum all the assigned ranks of the n baseline observations,
and let this sum be Sn.
(e) Obtain the critical value (C) from Table 1. When 12 monthly
data are available for both baseline and monitoring (i.e., n
= 12 and m = 12), the critical value C is 99.
(f) Compare C to Sn. If Sn is less than C, then the monitoring
loadings have exceeded the baseline loadings.
(2) Example Calculations for the Wilcoxon-Mann-Whitney Test
|
BASELINE DATA |
| 8.0 |
9.0 |
9.0 |
10.0 |
12.0 |
15.0 |
17.0 |
18.0 |
21.0 |
23.0 |
28.0 |
30.0 |
|
MONITORING DATA |
| 9.0 |
10.0 |
11.0 |
12.0 |
13.0 |
14.0 |
16.0 |
18.0 |
20.0 |
24.0 |
29.0 |
31.0 |
|
BASELINE RANKS |
| 1.0 |
3.0 |
3.0 |
5.5 |
8.5 |
12.0 |
14.0 |
15.5 |
18.0 |
19.0 |
21.0 |
23.0 |
|
MONITORING RANKS |
| 3.0 |
5.5 |
7.0 |
8.5 |
10.0 |
11.0 |
13.0 |
15.5 |
17.0 |
20.0 |
22.0 |
24.0 |
(3) Critical Values for the Wilcoxon-Mann-Whitney Test
(a) When n and m are less than 21, use Table 1.
In order to find the appropriate critical value, match column
with correct n (number of baseline observations) to row with
correct m (number of monitoring observations).*
Table 1 - Critical Values (C) of the
Wilcoxon-Mann-Whitney Test
(for a one-sided test at the 0.001
significance level)
n
m |
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
| 10 |
66 |
79 |
93 |
109 |
125 |
142 |
160 |
179 |
199 |
220 |
243 |
| 11 |
68 |
82 |
96 |
112 |
128 |
145 |
164 |
183 |
204 |
225 |
248 |
| 12 |
70 |
84 |
99 |
115 |
131 |
149 |
168 |
188 |
209 |
231 |
253 |
| 13 |
73 |
87 |
102 |
118 |
135 |
153 |
172 |
192 |
214 |
236 |
259 |
| 14 |
75 |
89 |
104 |
121 |
138 |
157 |
176 |
197 |
218 |
241 |
265 |
| 15 |
77 |
91 |
107 |
124 |
142 |
161 |
180 |
201 |
223 |
246 |
270 |
| 16 |
79 |
94 |
110 |
127 |
145 |
164 |
185 |
206 |
228 |
251 |
276 |
| 17 |
81 |
96 |
113 |
130 |
149 |
168 |
189 |
211 |
233 |
257 |
281 |
| 18 |
83 |
99 |
116 |
134 |
152 |
172 |
193 |
215 |
238 |
262 |
287 |
| 19 |
85 |
101 |
119 |
137 |
156 |
176 |
197 |
220 |
243 |
268 |
293 |
| 20 |
88 |
104 |
121 |
140 |
160 |
180 |
202 |
224 |
248 |
273 |
299 |
(b) When n or m is greater than 20 and there are few ties,
calculate an approximate critical value using the following formula
and round the result to the next larger integer. Let N = n + m.
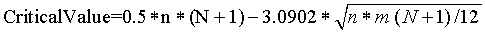
For example, this calculation provides a result of 295.76 for n
= m = 20, and a result of 96.476 for n = m = 12. Rounding up
produces approximate critical values of 296 and 97.
(c) When n or m is greater than 20 and there are many ties,
calculate an approximate critical value using the following formula
and round the result to the next larger integer. Let S be the sum
of the squares of the ranks or average ranks of all N observations.
Let N = n + m.
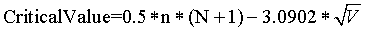
In the preceding formula, calculate V using
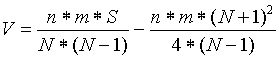
[67 FR
3408, Jan. 23, 2002]
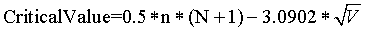
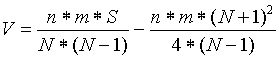 [67 FR
3408, Jan. 23, 2002]
[67 FR
3408, Jan. 23, 2002]